Enriching continuous Lagrange finite element approximation spaces using neural networks

In this work, we present a preliminary study combining two approaches in the context of solving PDEs: the classical finite element method (FEM) and more recent techniques based on neural networks. Indeed, in recent years, physics-informed neural networks (PINNs) have become particularly interesting for rapidly solving such problems, especially in high dimensions. However, their lack of accuracy is a significant drawback in this context, hence the interest in combining them with FEM, for which error estimators are already known. The complete pipeline proposed here, therefore, consists of modifying classical FEM approximation spaces by taking information from a prior, chosen here as the prediction of a neural network. On the one hand, this combination improves and certifies the prediction of neural networks to obtain a fast and accurate solution. On the other hand, error estimates are proven, showing that such strategies outperform classical ones by a factor that depends only on the quality of the prior. We validate our approach with numerical results obtained for this preliminary work on parametric problems with one-and two-dimensional geometries. They demonstrate that to achieve a fixed error target, a coarser mesh can be used with our enhanced FEM compared to the standard one, leading to reduced computation time, particularly for parametric problems.

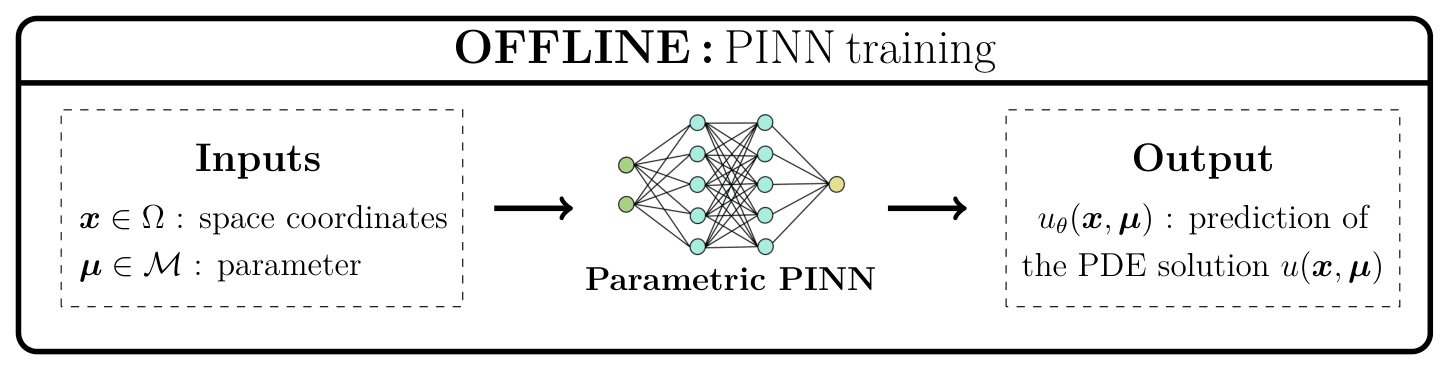
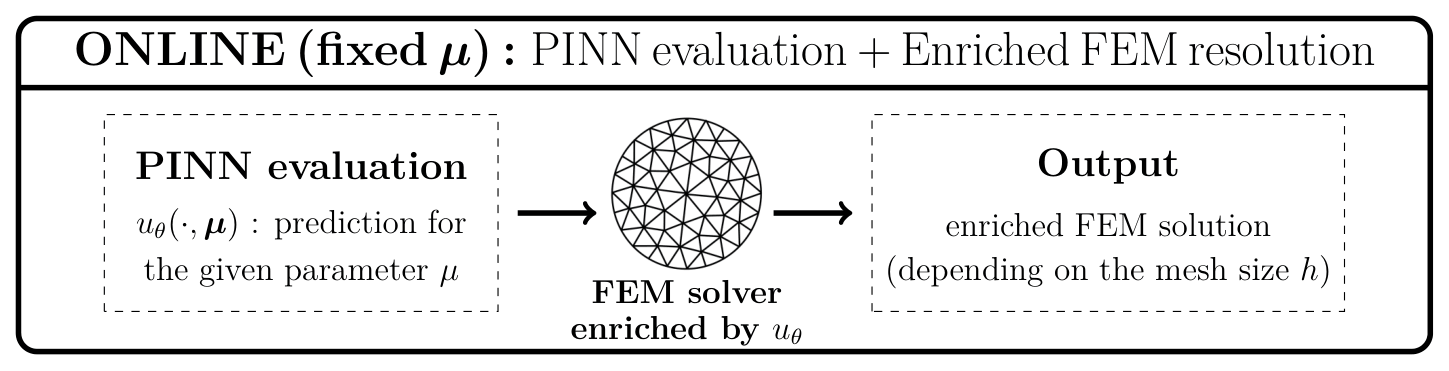
The following figures show the offline and online stages of the proposed approach.